Difference between revisions of "User:Regina/MYDrafts3"
(Created page with '=== Details === Semantics: Let X1, X2, …,Xn be the numbers in the sequence X and Y1, Y2, …,Ym be the numbers in the sequence Y. Then and . Moreover let , and where Γ is …') |
|||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
=== Details === | === Details === | ||
| − | + | The Student's test is related to the t-distribution. Its density function is | |
| − | + | ||
| − | + | <math> | |
| − | = | + | f(x,df)=\cfrac {\operatorname{\Gamma} \left ( \frac {df+1}{2} \right )} |
| − | + | { \sqrt{\pi df} \, \Gamma \left ( \frac {df} {2} \right )} \, | |
| + | \left ( 1 + \frac {x^2} {df} \right )^{-\left ( \frac {df+1}{2} \right )} | ||
| + | </math> | ||
| − | and | + | where <math>\Gamma</math> is the Gamma function and <math>df</math> the parameter ''degree of freedom''. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | and | + | ==== Paired Samples ==== |
| − | + | If type=1, TTEST calculates the p-value for paired samples. It uses the differences of the pairs. So in this case the data X and Y should have the same count n. | |
| − | TTEST returns | + | |
| − | ( | + | <math>\overline{X} = \frac{1}{n}\ \sum_{i=1}^n\, X_i \qquad |
| + | \overline{Y} = \frac{1}{n}\ \sum_{i=1}^n\, Y_i</math> | ||
| + | |||
| + | <math>s_{X-Y}^2 = \frac 1 {n-1} \sum_{i=1}^n \left ( (X_i -Y_i) - (\overline X - \overline Y ) \right )^2</math> | ||
| + | |||
| + | <math>t = \frac {\left | \overline X - \overline Y \right |} | ||
| + | {\sqrt { \frac {s_{X-Y}^2} n} }</math> | ||
| + | |||
| + | TTEST returns <math> tails \cdot \int_t^\infty f(x,n-1) \, dx </math> | ||
| + | |||
| + | ==== Unpaired Samples, Equal Variance ==== | ||
| + | |||
| + | If type = 2, TTEST calculates the p-value of a comparison of means for independent samples from populations with equal variance. Besides | ||
| + | |||
| + | <math>{s_X}^2=\tfrac 1 {n-1} \sum_{i=1}^n \left (X_i - \overline X \right )^2 \qquad | ||
| + | {s_Y}^2=\tfrac 1 {m-1} \sum_{i=1}^m \left (Y_i - \overline Y \right )^2 | ||
| + | </math> | ||
| + | |||
| + | it uses the pooled variance | ||
| + | |||
| + | <math>{s_P}^2 = \frac {(n-1) {s_X}^2 + (m-1) {s_Y}^2} {n-1+m-1} </math> | ||
and | and | ||
| − | TTEST returns . | + | <math>t = \frac {\left | \overline X - \overline Y \right |}{\sqrt { {s_P}^2(\frac 1 n + \frac 1 m)}}</math> |
| − | + | ||
| + | TTEST returns <math> tails \cdot \int_t^\infty f(x,n+m-2) \, dx </math> | ||
| + | |||
| + | |||
| + | ==== Unpaired Samples, Unequal Variances ==== | ||
| + | |||
| + | If type = 3, TTEST calculates the p-value of a comparison of means for independent samples from populations with not necessarily equal variances. | ||
| + | |||
| + | <math>t = \frac {\left | \overline X - \overline Y \right |}{\sqrt { \cfrac {{s_X}^2} n + \cfrac {{s_Y}^2} m}} | ||
| + | \qquad | ||
| + | \nu = \cfrac {\left ( \cfrac {{s_X}^2} n + \cfrac {{s_Y}^2} m \right )^2} | ||
| + | {\cfrac {\left (\cfrac {{s_X}^2} n \right )^2}{n-1} + \cfrac {\left ( \cfrac {{s_Y}^2} m \right)^2}{m-1}} | ||
| + | </math> | ||
| + | |||
| + | TTEST returns <math>\, tails \cdot \int_t^\infty f(x,\nu) \, dx </math> . | ||
| + | |||
| + | |||
| + | |||
| + | OpenOffice.org uses internally the regularized incomplete beta function to calculate the integral. | ||
| + | |||
| + | An empty element or an element of type ''string'' is ignored and in case paired samples its corresponding element in the other sample too. In contrast to other spreadsheet applications OpenOffice.org has no type ''boolean'' but treats ''false'' as 0 and ''true'' as 1. | ||
Latest revision as of 22:35, 31 March 2010
Contents
Details
The Student's test is related to the t-distribution. Its density function is
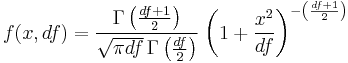
where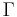 
is the Gamma function and 
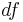the parameter degree of freedom.
Paired Samples
If type=1, TTEST calculates the p-value for paired samples. It uses the differences of the pairs. So in this case the data X and Y should have the same count n.
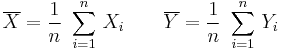
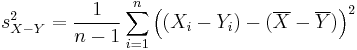
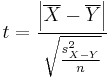
TTEST returns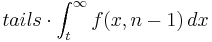 
Unpaired Samples, Equal Variance
If type = 2, TTEST calculates the p-value of a comparison of means for independent samples from populations with equal variance. Besides
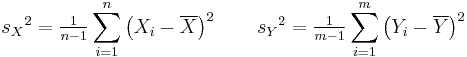
it uses the pooled variance
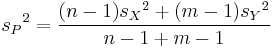
and
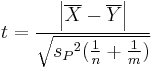
TTEST returns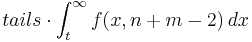 
Unpaired Samples, Unequal Variances
If type = 3, TTEST calculates the p-value of a comparison of means for independent samples from populations with not necessarily equal variances.
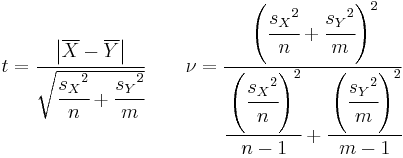
TTEST returns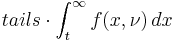 
.
OpenOffice.org uses internally the regularized incomplete beta function to calculate the integral.
An empty element or an element of type string is ignored and in case paired samples its corresponding element in the other sample too. In contrast to other spreadsheet applications OpenOffice.org has no type boolean but treats false as 0 and true as 1.
