Difference between revisions of "User:Regina/MYDrafts3"
(→type = 1) |
(→Details: (checkpoint save)) |
||
| Line 1: | Line 1: | ||
=== Details === | === Details === | ||
| − | + | The Student's test is related to the t-distribution. Its density function is | |
| − | + | ||
| + | <math> | ||
| + | f(x,df)=\cfrac {\operatorname{\Gamma} \left ( \frac {df+1}{2} \right )} | ||
| + | { \sqrt{\pi df} \, \Gamma \left ( \frac {df} {2} \right )} \, | ||
| + | \left ( 1 + \frac {x^2} {df} \right )^{-\left ( \frac {df+1}{2} \right )} | ||
| + | </math> | ||
| + | |||
| + | where <math>\Gamma</math> is the Gamma function and <math>df</math> the parameter ''degree of freedom''. | ||
| − | |||
==== Paired Samples ==== | ==== Paired Samples ==== | ||
If type=1, a paired Student's test is calculated. It uses the differences of the pairs. So in this case the data X and Y should have the same count n. | If type=1, a paired Student's test is calculated. It uses the differences of the pairs. So in this case the data X and Y should have the same count n. | ||
| − | <math>\overline{X} = \frac{1}{n}\ \sum_{i=1}^n\, X_i</math> | + | |
| − | <math> | + | <math>\overline{X} = \frac{1}{n}\ \sum_{i=1}^n\, X_i \qquad |
| + | \overline{Y} = \frac{1}{n}\ \sum_{i=1}^n\, Y_i</math> | ||
| + | |||
| + | <math>s_{X-Y}^2 = \frac 1 {n-1} \sum_{i=1}^n \left ( (X_i -Y_i) - (\overline X - \overline Y ) \right )^2</math> | ||
TTEST calculates the p-value for a paired-sample comparison of means test. Note that in this case due to the above constraints n=m. With | TTEST calculates the p-value for a paired-sample comparison of means test. Note that in this case due to the above constraints n=m. With | ||
Revision as of 20:31, 31 March 2010
Details
The Student's test is related to the t-distribution. Its density function is
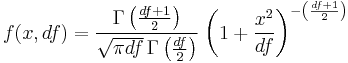
where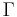 
is the Gamma function and 
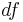the parameter degree of freedom.
Paired Samples
If type=1, a paired Student's test is calculated. It uses the differences of the pairs. So in this case the data X and Y should have the same count n.
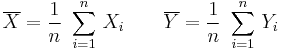
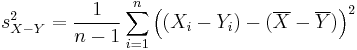
TTEST calculates the p-value for a paired-sample comparison of means test. Note that in this case due to the above constraints n=m. With
and
TTEST returns.
Unpaired Samples, Equal Variance
(2)If type = 2, TTEST calculates the p-value of a comparison of means for independent samples from populations with equal variance. With
and
==== Unpaired Samples, Not Necessarily Equal Variances
TTEST returns . (3)If type = 3, TTEST calculates the p-value of a comparison of means for independent samples from populations with not necessarily equal variances. With
and
TTEST returns . For an empty element or an element of type Text or Boolean in X the element at the corresponding position of Y is ignored, and vice versa.
